Section 3.1: The First Derivative Test


Objectives:

1. Students will be able to use the First Derivative Test to find relative extrema for differentiable functions.

Items to Review

1. Continuity
2. Critical Numbers
3. Relative Extrema
4. Increasing and Decreasing Functions


1. Main Idea of Continuity

                     Continuous


                     Continuous


                     Discontinuous



2. Main Idea of Critical Numbers


Definition of a Critical Number

Let \(f\) be defined at \(c\). If \(f'(c)=0\) or if \(f\) is not differentiable at \(c\), then \(c\) is a critical number of \(f\).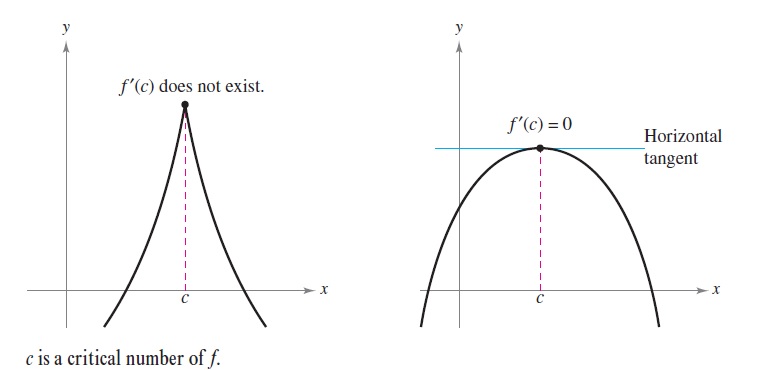


Main Ideas:

     1. \(f(c)\) must exist

     2. \(f'(c)=0\)

            or

     3. \(f'(c)\) does not exist.



Examples:


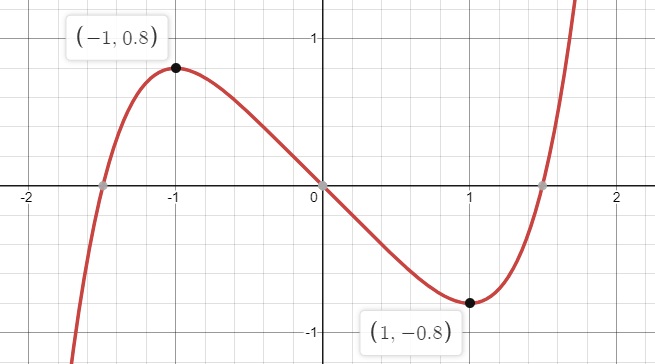
                     \(x=\pm1\)


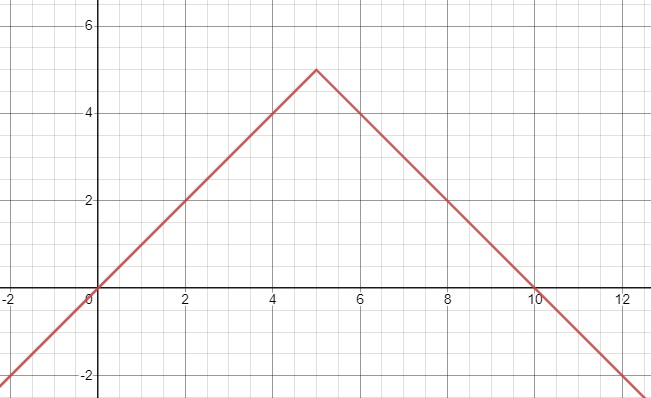
                     \(x=5\)




3. Main Idea of Relative Extrema

Definition of Relative Extrema
  1. If there is an open interval containing \(c\) on which \(f(c)\) is a maximum, then \(f(c)\) is called a relative maximum at \((c,f(c))\).
  2. If there is an open interval containing \(c\) on which \(f(c)\) is a minimum, then \(f(c)\) is called a relative minimum at \((c,f(c))\).


Examples:


                     \(0.8\) is a relative maximum and \(-0.8\) is a relative minimum


                     \(5\) is a relative maximum



4. Main Idea of Increasing and Decreasing Function




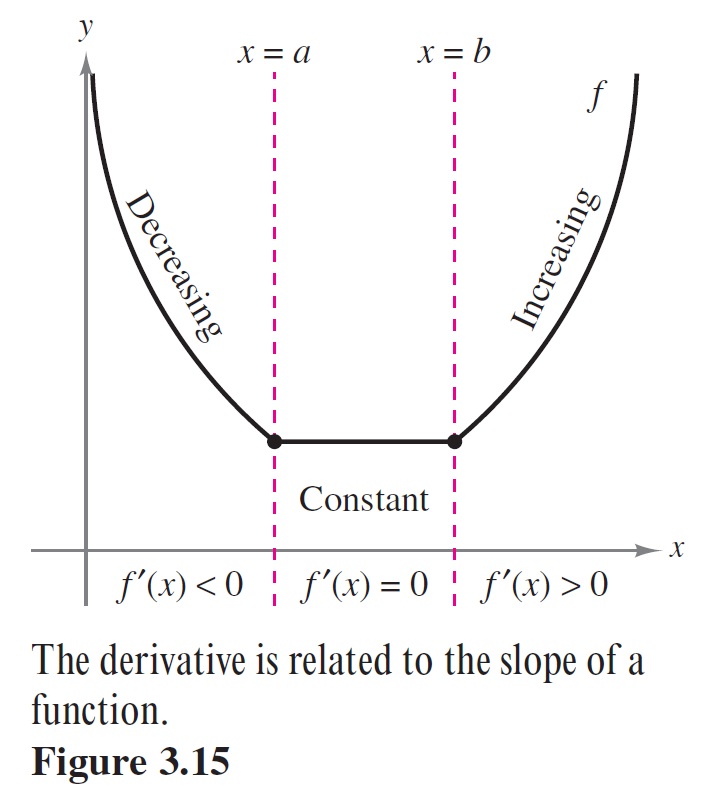
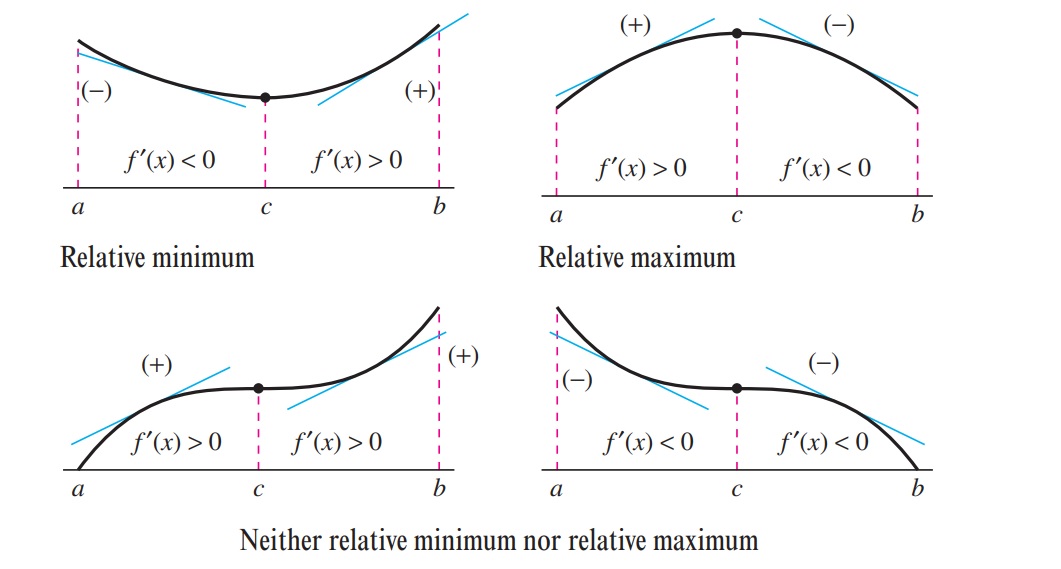
THEOREM 3.6: The First Derivative Test

Let \(c\) be a critical number of a function \(f\) that is continuous on an open interval \(I\) containing \(c\). If \(f\) is differentiable on the interval, except possible at \(c\), then \(f(c)\) can be classified as follows.
  1. If \(f'(x)\) changes from negative to positive at \(c\), then \(f\) has a relative minimum at \((c,f(c))\).
  2. If \(f'(x)\) changes from a positive to negative at \(c\), then \(f\) has a relative maximum at \((c,f(c))\).
  3. If \(f'(x)\) is positive on both sides of \(c\) or negative on both sides of \(c\), then \(f(c)\) is neither a relative maximum nor a relative minimum.




Steps to Utilizing The First Derivative Test to Find Relative Maximums or Minimums

Step 1: Ensure the function is continuous on the interval in question.

Step 2: Differentiate the function

Step 3: Find the critical values by determining where the derivative is undefined or equal to zero

Step 4: Identify the intervals between the critical values

Step 5: Pick a an \(x\)-value in each of those intervals and use the derivative of the function to test if the function is increasing or decreasing on those intervals

Step 6: Find the \(y\)-coordinate of the critical values that indicate a relative maximum or minimum is present. Those \(y\)-coordinates are going to be your relative maximum or minimum.



Use The First Derivative Test to find all the relative maximum and minimum for the following functions.

Example 1: \(f(x)=\frac{x^5-5x}{5}\)




Example 2: \(f(x)=5-|x-5|\)